 By: Paula Beatriz Morales Bañuelos
By: Paula Beatriz Morales Bañuelos
and Jorge Omar Moreno Treviño
The valuation of financial statements is fundamental for understanding the nature and dynamics of companies. Among the elements that pose the greatest difficulty in determining the value of the company, capital cost is basic for estimating and calculating the various items of the financial statements. This valuation can be somewhat challenging when the company operates in an emerging economy, because its situation may be incompatible with the methods applied in more developed markets.
The objetive of this article is to show the reader the many options that accountants and management have for determining the discount rate that best approximates the opportunity cost of the capital of the entity or company (hereinafter, capital cost), taking into account its particular characteristics, the economic situation in the country, and the type of transaction being carried out. Specifically, this paper focuses on methods that are compatible with the cases of companies that operate in emerging markets like Mexico.
According to the Mexican financial reporting standards (Mexican FRS), particularly FRS A-6, Recognition and Valuation, the fair value “represents the amount of cash or equivalent that market participants would be willing to exchange for the purchase or sale of an asset, or to assume or settle a liability, in a transaction between interested, disposed and informed parties, in a market of free competition. When no exchange value is available for the transaction, it should be estimated using valuation techniques.”
Specifically, the standards define the present value technique as a tool for valuation based on expected future cash flows, discounted at an appropriate discount rate. This discount rate should “observe: a) the yield investors demand on investments that will generate cash flow in the equivalent quantities, term and risk profile to those that the entity expects to obtain from the asset, reportable units, or cash generating unit, or b) the market rate to which the entity has access for settling its liabilities.” In other words, the rate in question should be such that it would lead to the capitalization cost of the company.
Given these elements, both FRS A-6 and traditional financial theory recommend using the weighted average capital cost (WACC) as the discount rate.
WACC has various components, which are expressed as follows (Equation 1):

Where:
- Kd* is the cost of debt, which is measured using the implied rate on future outlays for the payment of interests and principal, less the tax benefit provided by the deductible portion of interest expense
- VD is the market value of the debt
- VA is the market value of capital stock
- Ka is the minimum rate of return shareholders expect in accordance with the company’s risk.
In Equation 1, Ka evaluates the investment risk cost, which can be estimated though the capital asset pricing model (CAPM) which is used to determine the ratio of risk to return. If we assume that there is competitive balance in the securities market, the model theoretically relates the rate of return expected by shareholders of the company as the sum of the risk-free rate (premium for the change from consumption today to consumption tomorrow), plus a risk premium (compensation for the risk of taking investment) (Equation 2). Particularly:
Where:
- E(rj) is the expected return on investment.
- Rf is the risk-free rate (an instrument considered risk-free has no risk of default, meaning there is no risk that the issuer will fail to make payment of interest or principal when the instrument matures).
- E(rm) is the expected return on the market portfolio. “The market portfolio contains all the existing risky assets in the international economic system in proportion to what its value represents with respect to the total value of the rest of the assets” (Haugen, 2000).
- ?j is the base of the company and describes the stock’s response to changes in the market portfolio. The beta is defined by the following formula (Equation 3):
Where: rj and rm symbolize the returns of company j and the market, respectively, cov(rj,rm) is the covariance of the returns rj and rm, and ?2(rm) is the market return variance..
Traditionally, the estimation of employs various statistical and econometric methods to determine its value using securities market data (Berndt, 1991).
The beta of a publicly-traded company can be calculated using the above formula, or more elaborate methods using the market price of the stock; while private companies can proxy their beta based on the beta of their industry or comparable firms, adjusting it for the risk of the company or project analyzed.
The debt and capital market values for a company that is not publicly traded can be determined using other similar countries in the respective industry as a benchmark, or the proportions of debt and capital in an objective capital structure (Copeland et al., 2000).
Although the CAPM model is a solid method from the theoretic standpoint, and its empirical implications yield a series of interesting results in terms of the breakdown of risk into the portion that is systemic and the portion that is idiosyncratic for each company, it continues to have its detractors.
The most recent critiques on the use of the CAPM model for emerging markets (Pereiro, 2002) focus on both the assumptions on which it is based (competitive balance in the securities market and complete information from agents), and on the statistical and econometric methods used to calculate it. For example, as Godfrey and Espinosa (1996) point out, recent studies have empirically found a negative beta, and even for some stocks, a beta of zero, which would indicate that the assets serve as “hedges” against market risk, in the former case, or are assets free of systemic risk, in the latter.
Another criticism is that, in principle, CAPM is a better fit in developed markets in which it is possible to better diversify assets and reduce non-systemic risk. This is closely related to the theoretic assumptions that sustain the equation of competitive balance. The more developed the financial market is, the more information flows between a larger number of buyers and sellers, which allows prices and returns on assets to adjust in equilibrium, according to the premises of the original CAPM model. But this situation is not necessarily present in emerging markets in which information is expensive or the costs of trading on the securities market are significant.
In addition, emerging markets, the data time series necessary to estimate the beta values in CAPM are small or nonexistent, and it can be expensive to obtain them.
What alternatives to CAPM model are there to approximate the cost of capital stock, particularly in emerging markets like Mexico? In the following section, we will present some models that expand on and adapt CAPM to our environment.
1) CAPM global variant
In recent decades, the integration of international financial markets has made it increasingly necessary to incorporate the variable globalization in traditional models for studying investment alternatives. According to this factor, an agent or institution can invest anywhere in the world. Thus, we can develop an adjustment of CAPM as follows (Equation 4):
Where:
- Ka is the equity cost of capital
- RfG is the global risk-free rate. Generally US bond rates are taken as a reference.
- ?LG is the beta of a local company calculated with the global market Index, once again using the US indexes a reference, under the assumption that the US is a large, efficient and developed market.
- RMG is the global market yield.
In this model, we have assumed that the value of the assets is not correlated with exchange rates. There is abundant empirical evidence to show that the covariance between stock returns and exchange rate movements is very slight. The model may be accurate in developed markets, but not necessarily in the emerging markets, where country risk remains as a very important variable.
2) CAPM local variant
When financial markets are integrated, country risk is irrelevant, because portfolios must be highly diversified. Nevertheless, according to a survey by Keck et al. (1998), only 5% of respondents believe that financial markets are fully integrated. Thus, when there is a segmentation of financial markets, analysts propose the following variant of CAPM, adapted to the local environment (Equation 5):
Where:
- Ka is the equity cost of capital
- RfL is the local risk-free rate, which is composed of the global risk-free rate and the country risk premium
- ?LL is the beta of the local company, calculated with the local market index
- RML is the return on the local market index
Pereiro (2002) proposes that stock performance may be more closely linked to the volatility of the local economy than with fluctuations and trends in the corresponding international industry. In other words, this indicates that the local CAPM tends to overestimate risk, because the market index includes a part of the country risk.
In this respect, Erb et al. (1995) conducted a study of more than 40 developed and emerging economies and confirmed that country risk explains an average of 40% of the variation in the market yields, while the market risk of the stocks explained the remaining 60%, so the following model corrects this problem.
3) Adjusted CAPM local variant
This new model corrects the above alternative focusing on systemic risk premium. It takes a factor (1-Ri2) in which Ri2 is the determination coefficient of the regression between the volatility of the local company’s returns and the variation in the country return (Equation 6):
The considerable volatility of emerging markets makes very difficult to calculate the long-term market premium and betas, since both are highly unstable over time and an historic average tends to be unreliable or unavailable. Because of this problem, analysts prefer a more flexible model that incorporates elements of the previous alternatives.
4) Hybrid adjusted CAPM variant
This fourth alternative of the CAPM model calibrates the global market premium with the domestic market using the local beta. This parameter is the sensitivity of stock returns in the local economy to global returns (Godfrey and Espinosa, 1996). This model, as its name indicates, is hybrid, because it combines global and local risk parameters, as shown below (Equation 7):
Where:
- BCLG is the slope of the regression between the local market index and the global market Index
- BGG is the average beta of comparable companies listed on the global market
- R2 is the determination coefficient of the regression between the volatility of the local market stock with the variation in country risk
Here, too R2 can be interpreted as the variance in the volatility of the local stock market that is explained by country risk.
- Example
Example
Having presented the models, and to illustrate the value of knowing these alternatives, we decided to carry out an empirical analysis of a Mexican services company in the education industry, projecting its revenues for the period from 2011 to 2020, in order to obtain discounted free cash flow as of 2011, and later, discounted free cash flow for stockholders into 2011, to estimate the price of the stock, as well as the multiple of market price (forecast or valuation) to the book value of stockholders’ equity (P/BV) as of 2011 and compare these results with the industry multiple for the same fiscal year according to each model, beginning with the traditional CAPM and ending with the hybrid model. In this analysis, the projected cash flow was the same for every scenario; the only variation was the results of the equity cost of capital, according to what each method requires for its calculation (table 1).
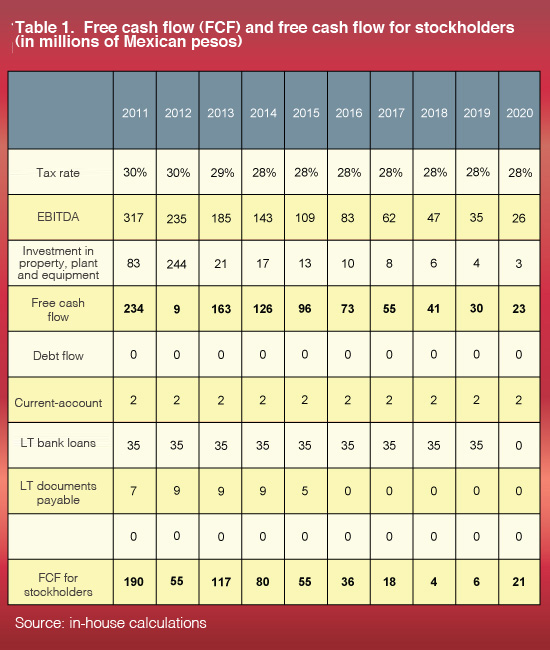
The results of each model are shown in table 2. Note that because only one company was considered, the results apply only to this company and cannot be generalized, because the circumstances of each industry and each entity vary considerably.
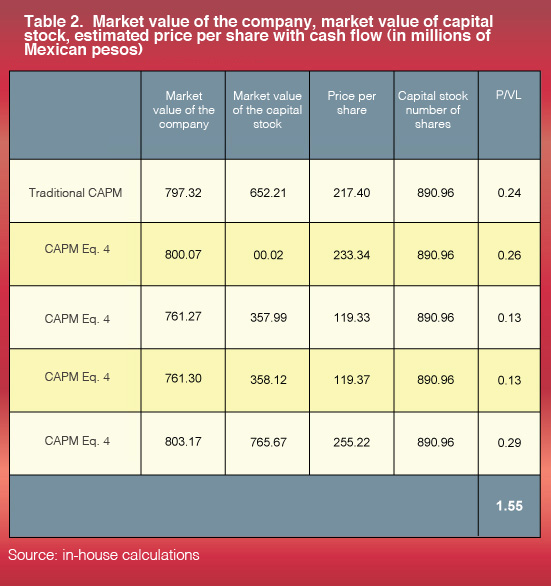
Although, as we can see, the ratio of the stock price to the book value of stockholders’ equity (P/BV) estimated using discounted cash flows is very different from that of the industry using any of the models, the one that offers the best result is the price estimated using the hybrid variant of adjusted CAPM, which, as we explained earlier, calibrates the effect of the global market with the domestic market and attenuates the incorporation of country risk.
We should stress that this result cannot be extrapolated to other industries or companies, since the models were tested on a single company. In this case, the local variants underestimated the value of the stock price, while the global and hybrid variants overestimated it, taking as a point of reference the result from the traditional CAPM. Thus, to answer the question of whether we should continue applying the traditional CAPM model, it is hard to generalize. Every company should consider the type of transactions it carries out, whether they are global, local or hybrid, and the economic situation of the country and the industry, and decide which model is most appropriate.
To conclude, it is crucial that we understand the role of the analyst or public accountant in calculating or backing the models and assumptions that each entity uses to determine a reasonable value through financial techniques. The person who prepares the accounting and valuation is responsible for verifying, among other aspects, why a given model may offer the best results, if the premises applied in preparing the cash flows are reasonable given the company’s situation and that of the economy at large and, finally, whether the assumptions applied to determine the discount rates are acceptable and verifiable. Thus, with an informed criterion that identifies the elements associated with each capital cost model, the accountant can determine whether the fair value presents useful and reliable information for the users of the financial statements, who require that information in order to efficiently make decisions.?
References
- Berndt, E. (1991). The Practice of Econometrics: Classic and Contemporary. Addison-Wesley.
- Copeland, T., Koller, T. y Murrin, J. (2000). Valuation: Measuring and Managing the Value of Companies. John Wiley & Sons, Inc. 3ª. ed.
- Erb, C.B., Harvey, C.R. y Viskanta, T.E. (1995). Country Risk and Global Equity Selection. The Journal of Portfolio Management, pp. 74-83.
- Godfrey, S. y Espinosa, R. (1996). A practical Approach to Calculating Cost of Equity for Investments in Emerging Markets. Journal of Applied Corporate Finance, 12 (3), pp. 14-28.
- Haugen, R. (2000). Modern Investment Theory. Prentice Hall. 5a. ed.
- Keck, T., Levengood, E. y Longfield, A. (1998). Using Discounted Flow Analysis in a International Setting: A Survey of Issues in Modeling the Cost of Capital. Journal of Applied Corporate Finance, 12 (3), pp. 63-72.
- Pereiro, L. (2002). Valuation of Companies in Emerging Markets: A Practical Approach. John Wiley & Sons, Inc.
Fuentes electrónicas
- Página de Internet del Banco de México consultada en febrero de 2012.
- Página de Internet del Banco Nacional de México consultada en febrero de 2012.
- Página de Internet de Damodaran Online consultada en marzo de 2012.
- Página de Internet de Yahoo Finance consultada en febrero de 2012.
Estimating Reasonable Value and Capital Cost in Emerging Markets
and Jorge Omar Moreno Treviño
The valuation of financial statements is fundamental for understanding the nature and dynamics of companies. Among the elements that pose the greatest difficulty in determining the value of the company, capital cost is basic for estimating and calculating the various items of the financial statements. This valuation can be somewhat challenging when the company operates in an emerging economy, because its situation may be incompatible with the methods applied in more developed markets.
The objetive of this article is to show the reader the many options that accountants and management have for determining the discount rate that best approximates the opportunity cost of the capital of the entity or company (hereinafter, capital cost), taking into account its particular characteristics, the economic situation in the country, and the type of transaction being carried out. Specifically, this paper focuses on methods that are compatible with the cases of companies that operate in emerging markets like Mexico.
According to the Mexican financial reporting standards (Mexican FRS), particularly FRS A-6, Recognition and Valuation, the fair value “represents the amount of cash or equivalent that market participants would be willing to exchange for the purchase or sale of an asset, or to assume or settle a liability, in a transaction between interested, disposed and informed parties, in a market of free competition. When no exchange value is available for the transaction, it should be estimated using valuation techniques.”
Specifically, the standards define the present value technique as a tool for valuation based on expected future cash flows, discounted at an appropriate discount rate. This discount rate should “observe: a) the yield investors demand on investments that will generate cash flow in the equivalent quantities, term and risk profile to those that the entity expects to obtain from the asset, reportable units, or cash generating unit, or b) the market rate to which the entity has access for settling its liabilities.” In other words, the rate in question should be such that it would lead to the capitalization cost of the company.
Given these elements, both FRS A-6 and traditional financial theory recommend using the weighted average capital cost (WACC) as the discount rate.
WACC has various components, which are expressed as follows (Equation 1):
Where:
In Equation 1, Ka evaluates the investment risk cost, which can be estimated though the capital asset pricing model (CAPM) which is used to determine the ratio of risk to return. If we assume that there is competitive balance in the securities market, the model theoretically relates the rate of return expected by shareholders of the company as the sum of the risk-free rate (premium for the change from consumption today to consumption tomorrow), plus a risk premium (compensation for the risk of taking investment) (Equation 2). Particularly:
Where:
Where: rj and rm symbolize the returns of company j and the market, respectively, cov(rj,rm) is the covariance of the returns rj and rm, and ?2(rm) is the market return variance..
Traditionally, the estimation of employs various statistical and econometric methods to determine its value using securities market data (Berndt, 1991).
The beta of a publicly-traded company can be calculated using the above formula, or more elaborate methods using the market price of the stock; while private companies can proxy their beta based on the beta of their industry or comparable firms, adjusting it for the risk of the company or project analyzed.
The debt and capital market values for a company that is not publicly traded can be determined using other similar countries in the respective industry as a benchmark, or the proportions of debt and capital in an objective capital structure (Copeland et al., 2000).
Although the CAPM model is a solid method from the theoretic standpoint, and its empirical implications yield a series of interesting results in terms of the breakdown of risk into the portion that is systemic and the portion that is idiosyncratic for each company, it continues to have its detractors.
The most recent critiques on the use of the CAPM model for emerging markets (Pereiro, 2002) focus on both the assumptions on which it is based (competitive balance in the securities market and complete information from agents), and on the statistical and econometric methods used to calculate it. For example, as Godfrey and Espinosa (1996) point out, recent studies have empirically found a negative beta, and even for some stocks, a beta of zero, which would indicate that the assets serve as “hedges” against market risk, in the former case, or are assets free of systemic risk, in the latter.
Another criticism is that, in principle, CAPM is a better fit in developed markets in which it is possible to better diversify assets and reduce non-systemic risk. This is closely related to the theoretic assumptions that sustain the equation of competitive balance. The more developed the financial market is, the more information flows between a larger number of buyers and sellers, which allows prices and returns on assets to adjust in equilibrium, according to the premises of the original CAPM model. But this situation is not necessarily present in emerging markets in which information is expensive or the costs of trading on the securities market are significant.
In addition, emerging markets, the data time series necessary to estimate the beta values in CAPM are small or nonexistent, and it can be expensive to obtain them.
What alternatives to CAPM model are there to approximate the cost of capital stock, particularly in emerging markets like Mexico? In the following section, we will present some models that expand on and adapt CAPM to our environment.
1) CAPM global variant
In recent decades, the integration of international financial markets has made it increasingly necessary to incorporate the variable globalization in traditional models for studying investment alternatives. According to this factor, an agent or institution can invest anywhere in the world. Thus, we can develop an adjustment of CAPM as follows (Equation 4):
Where:
In this model, we have assumed that the value of the assets is not correlated with exchange rates. There is abundant empirical evidence to show that the covariance between stock returns and exchange rate movements is very slight. The model may be accurate in developed markets, but not necessarily in the emerging markets, where country risk remains as a very important variable.
2) CAPM local variant
When financial markets are integrated, country risk is irrelevant, because portfolios must be highly diversified. Nevertheless, according to a survey by Keck et al. (1998), only 5% of respondents believe that financial markets are fully integrated. Thus, when there is a segmentation of financial markets, analysts propose the following variant of CAPM, adapted to the local environment (Equation 5):
Where:
Pereiro (2002) proposes that stock performance may be more closely linked to the volatility of the local economy than with fluctuations and trends in the corresponding international industry. In other words, this indicates that the local CAPM tends to overestimate risk, because the market index includes a part of the country risk.
In this respect, Erb et al. (1995) conducted a study of more than 40 developed and emerging economies and confirmed that country risk explains an average of 40% of the variation in the market yields, while the market risk of the stocks explained the remaining 60%, so the following model corrects this problem.
3) Adjusted CAPM local variant
This new model corrects the above alternative focusing on systemic risk premium. It takes a factor (1-Ri2) in which Ri2 is the determination coefficient of the regression between the volatility of the local company’s returns and the variation in the country return (Equation 6):
The considerable volatility of emerging markets makes very difficult to calculate the long-term market premium and betas, since both are highly unstable over time and an historic average tends to be unreliable or unavailable. Because of this problem, analysts prefer a more flexible model that incorporates elements of the previous alternatives.
4) Hybrid adjusted CAPM variant
This fourth alternative of the CAPM model calibrates the global market premium with the domestic market using the local beta. This parameter is the sensitivity of stock returns in the local economy to global returns (Godfrey and Espinosa, 1996). This model, as its name indicates, is hybrid, because it combines global and local risk parameters, as shown below (Equation 7):
Where:
Here, too R2 can be interpreted as the variance in the volatility of the local stock market that is explained by country risk.
Example
Having presented the models, and to illustrate the value of knowing these alternatives, we decided to carry out an empirical analysis of a Mexican services company in the education industry, projecting its revenues for the period from 2011 to 2020, in order to obtain discounted free cash flow as of 2011, and later, discounted free cash flow for stockholders into 2011, to estimate the price of the stock, as well as the multiple of market price (forecast or valuation) to the book value of stockholders’ equity (P/BV) as of 2011 and compare these results with the industry multiple for the same fiscal year according to each model, beginning with the traditional CAPM and ending with the hybrid model. In this analysis, the projected cash flow was the same for every scenario; the only variation was the results of the equity cost of capital, according to what each method requires for its calculation (table 1).
The results of each model are shown in table 2. Note that because only one company was considered, the results apply only to this company and cannot be generalized, because the circumstances of each industry and each entity vary considerably.
Although, as we can see, the ratio of the stock price to the book value of stockholders’ equity (P/BV) estimated using discounted cash flows is very different from that of the industry using any of the models, the one that offers the best result is the price estimated using the hybrid variant of adjusted CAPM, which, as we explained earlier, calibrates the effect of the global market with the domestic market and attenuates the incorporation of country risk.
We should stress that this result cannot be extrapolated to other industries or companies, since the models were tested on a single company. In this case, the local variants underestimated the value of the stock price, while the global and hybrid variants overestimated it, taking as a point of reference the result from the traditional CAPM. Thus, to answer the question of whether we should continue applying the traditional CAPM model, it is hard to generalize. Every company should consider the type of transactions it carries out, whether they are global, local or hybrid, and the economic situation of the country and the industry, and decide which model is most appropriate.
To conclude, it is crucial that we understand the role of the analyst or public accountant in calculating or backing the models and assumptions that each entity uses to determine a reasonable value through financial techniques. The person who prepares the accounting and valuation is responsible for verifying, among other aspects, why a given model may offer the best results, if the premises applied in preparing the cash flows are reasonable given the company’s situation and that of the economy at large and, finally, whether the assumptions applied to determine the discount rates are acceptable and verifiable. Thus, with an informed criterion that identifies the elements associated with each capital cost model, the accountant can determine whether the fair value presents useful and reliable information for the users of the financial statements, who require that information in order to efficiently make decisions.?
References
Fuentes electrónicas